GLYPH

How mass moves mass in weightlifting

by · May 29, 2019

That weightlifting is the art of defeating gravity may seem a statement of the obvious. It is very rewarding however, as all battles, to consider the nature of the adversary. Its relentless nature means that man can only win for a limited time.
-D.W. Grieve, from “The Defeat of Gravity in Weight Lifting“

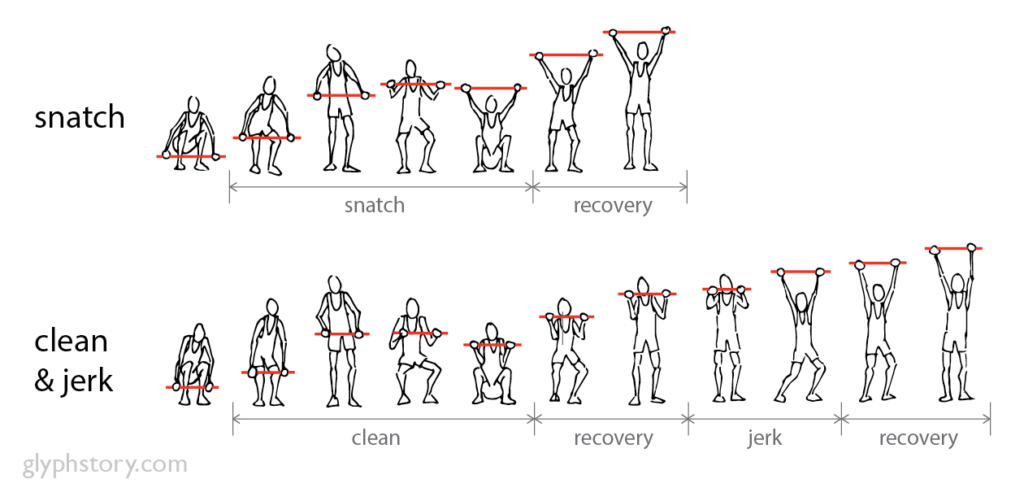
Mass moves mass. If you’ve ever spent time in a powerlifting or CrossFit gym you likely have heard this “hot take” about the reason why the big boys and girls are moving big weight. But you’ve probably also seen the slight ninja with perfect technique who’s lifting twice their own bodyweight. So, then, does mass indeed move mass? A data set to address this question exists in the world records of the Olympic total lift, which are categorized by weight class. The total lift consists of the two modern Olympic weightlifting movements – the snatch and the clean & jerk – which are performed in the same competition and summed to give the total.

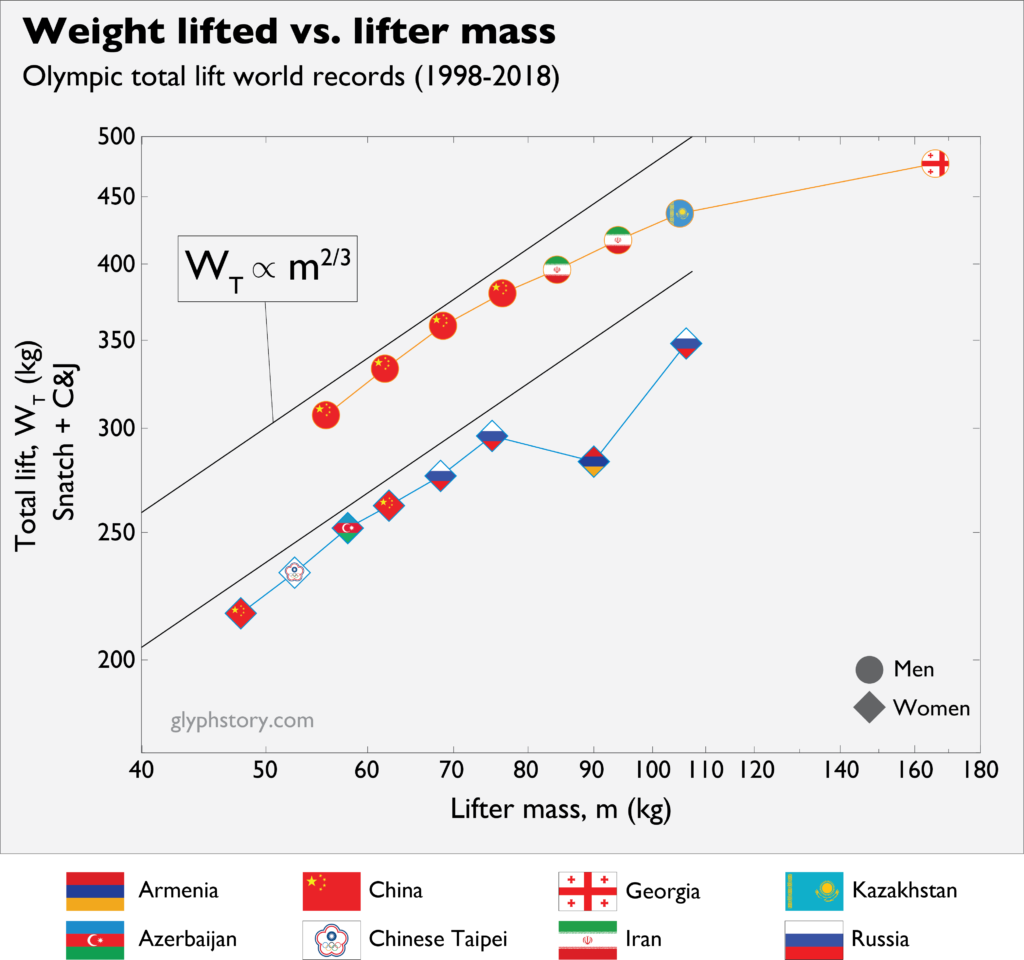
In the snatch, the lifter uses a wide grip and lifts the barbell from the ground to overhead in one continuous motion, “dropping” under the bar in a squat position before standing back up with the weight overhead.  In the clean & jerk, the barbell is pulled from the ground to the shoulders (the clean), and then from the standing position the lifter drives under the bar with one foot forward and one back to lock the bar overhead (the jerk).  These movements simultaneously require a great deal of technique and explosive force.

In the time period from 1998 to 2018, records were kept in eight body weight classes for both women and men ranging from Bantamweight (48 kg women / 56 kg men) to Super Heavyweight (90+ kg women / 105+ kg men). When we plot the world records for total lift as a function of body mass of the lifter, the first thing that jumps out is that the 1998 to 2018 time period was decidedly dominated by men and women from the Eastern Hemisphere. What is also clear is that there is a consistent increase in weight lifted with increasing weight of the lifter (with the exception of one outlier data point in the women’s 90 kg category). So evidently, mass does moves mass in weightlifting; but is all mass created equal? And if you’re planning to bulk up, what what kind of returns should you expect on that investment?

To perform an Olympic lift requires that the lifter put a force on the barbell to overcome gravity. This force is initiated by the feet at the ground and is carried through the body in a series of kinetic motions and ultimately delivered at the barbell through the hands. The component in the body responsible for producing force is muscle (namely, skeletal muscle). So we can more accurately say that muscle mass moves mass. In humans, as in all mammals, the stress that muscle can sustain is a constant, unvarying number1. Stress (\sigma) is defined as force (F) per unit cross-sectional area (A). Given that muscle stress is a constant, the muscle force scales linearly with cross-sectional area. Therefore, to produce more force with our muscles, we must increase their cross-sectional area; that is, we must “get swoll”. Now, how does this relate to mass?

The mass (m) of a muscle is proportional to its volume (V). When humans increase their muscle volume, an equal increase in length (L) is experienced in all three dimensions of the muscle2. The length change in any one direction thus scales with mass to the \frac{1}{3} power. The increase in muscle cross-sectional area A is proportional to length squared, and as a result area is proportional to mass to the \frac{2}{3} power: A \propto m^{2/3}. Therefore, the increase in muscle force is not linear with increasing muscle mass; rather, force increases with mass to the \frac{2}{3} power.

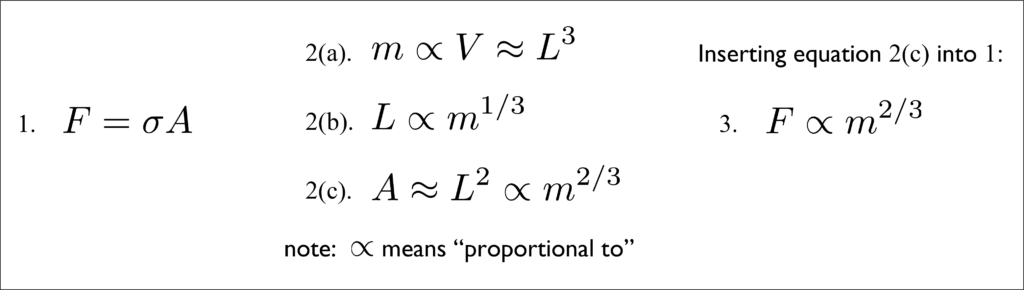
Now, back to the graph of weight lifted vs. lifter mass. Because force produced by the muscles should be directly related to the weight that can be lifted, we should expect that the total weight lifted W_T scale with lifter mass to the \frac{2}{3} power, W_T \propto m^{2/3}. This is easy to visualize on the weight lifted vs. lifter mass figure, which is plotted on log-log axes. The solid black lines have slope \frac{2}{3}, reflecting a dependence of weight lifted (via muscle force) on body mass to the \frac{2}{3} power. Most of the men’s and women’s weight classes track very well with this trend. As the lifter mass becomes very high, there are some diminishing returns on the relationship between body mass and weight lifted. We will discuss this deviation in an upcoming article on the Sinclair coefficients.

The bottom line: muscle mass moves barbell mass, but it’s not a one-for-one return.

*The scaling analysis between muscle force and muscle mass follows from a derivation in the book On Size and Life, by Thomas A. McMahon and John Tyler Bonner. (Scientific American Library, 1983). This is a beautiful book full of elegant analyses.

**Data sourced from: Lift Up, International Weightlifting Federation, International Weightlifting Results Project and Wikipedia.

  1. Madden, John DW, et al. “Artificial muscle technology: physical principles and naval prospects.” IEEE Journal of oceanic engineering 29.3 (2004): 706-728.
  2. McMahon, Thomas A., and John Tyler Bonner. On size and life. Scientific American Library, 1983.

You may also like...