Should you pay for mortgage points?
Mortgage points – a bet with the bank.
The housing market is a little crazy1 at the moment. There are indications2 that the growth in home prices will slow down, both actual data3 and anecdata4 suggest that there are a lot of people doing mortgage math at the moment. There are a lot of calculators5 out there to help you do this, but when my wife and I bought a house, there was one aspect of the process that I did not feel was done correctly and completely anywhere.
When you apply for a mortgage, most lenders let you pay more front to reduce the interest rate. These payments are known as “points”, and typically cost 1% of the value of the loan. If you keep paying that loan long enough, the money you save because of the reduced interest rate becomes larger than the amount of money you paid up front for the points, and you pay less money in total for the house. Hooray!
However, paying for the points is effectively a bet that you are making with the bank. You are betting that you will remain in the house without refinancing for more time than it takes for that lower interest rate to pay for itself. So, how much time does it take to pay off the points? It depends on the base rate, the number of points, and the interest rate discount that you get per point. Although this is relatively easy to calculate, most online calculators make a incorrect (but honest) assumption. We’ll first develop the payoff time in this wrong way before explaining the right way to think about it.
The wrong way
The monthly payment ![]() on a loan of value
on a loan of value ![]() is
is
![]()
where ![]() is the monthly interest rate and
is the monthly interest rate and ![]() is the full term of the loan in months. Here, we will take
is the full term of the loan in months. Here, we will take ![]() to be the base monthly rate, which we will modify with points. If you want to calculate the monthly payment on that same loan amount, but where you have paid some points, you get the modified payment
to be the base monthly rate, which we will modify with points. If you want to calculate the monthly payment on that same loan amount, but where you have paid some points, you get the modified payment
![]()
where ![]() is the change in monthly rate from paying the points. Because you’re shrinking the interest rate,
is the change in monthly rate from paying the points. Because you’re shrinking the interest rate, ![]() . In order to get that change in rate, you had to pay the bank
. In order to get that change in rate, you had to pay the bank ![]() . You would like to know how many months will it take for the difference in payments to equal the cost of the points. You get there by solving6 the expression
. You would like to know how many months will it take for the difference in payments to equal the cost of the points. You get there by solving6 the expression
![]()
for ![]() . This is a general expression in four parameters — the term in months
. This is a general expression in four parameters — the term in months ![]() , the monthly rate
, the monthly rate ![]() , the change in rate
, the change in rate ![]() and the payment for all points
and the payment for all points ![]() — but we can simplify to two parameters by taking the values
— but we can simplify to two parameters by taking the values
![]()
![]()
![]()
where ![]() is the number of points paid for. The value for
is the number of points paid for. The value for ![]() is more-or-less universal, and the value for
is more-or-less universal, and the value for ![]() is very common. It is possible to (somewhat) regeneralize
is very common. It is possible to (somewhat) regeneralize ![]() using our results, so keep reading if you’re not getting 0.25% APR per point from your lender. Using
using our results, so keep reading if you’re not getting 0.25% APR per point from your lender. Using ![]() means that we’re talking about a 30-year fixed rate mortgage. Of course, the reason to simplify to two parameters is that it allows us to express the payback time on a contour map, which as we all know is the apotheosis of scientific communication. See below.
means that we’re talking about a 30-year fixed rate mortgage. Of course, the reason to simplify to two parameters is that it allows us to express the payback time on a contour map, which as we all know is the apotheosis of scientific communication. See below.
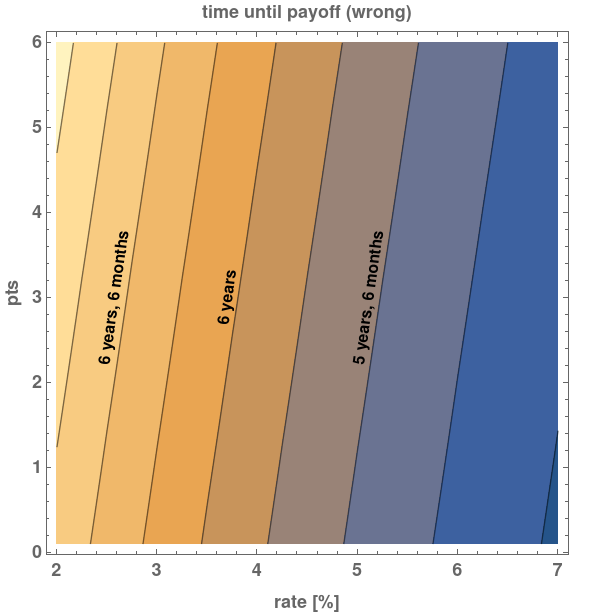
In Fig.1, we see that the payback time is a little over 6 years for a 3.45% APR, which is the national average7 at the time of writing for a 30-year fixed rate mortgage. There are a couple of other notable things about the figure. First, the payback time decreases with increasing base rate. Second, the payback time increases as the number of points purchased increases. We’ll revisit these when we show the right way to find the payback time, after we discuss…
Why the above is wrong
I keep saying it, but what is actually wrong with the above method? The issue comes at the very beginning, when we used the same loan amount ![]() for both the “points” and “no points” calculations. This isn’t crazy, but it’s also not quite right. When you go to purchase a house which costs
for both the “points” and “no points” calculations. This isn’t crazy, but it’s also not quite right. When you go to purchase a house which costs ![]() , you have some amount of cash
, you have some amount of cash ![]() which you can apply to a combination of the down payment and the points. For the “no points” case, the loan amount
which you can apply to a combination of the down payment and the points. For the “no points” case, the loan amount
![]()
but if you want to buy points, the amount available for the down payment decreases, which increases the loan amount such that
![]()
To do this right, we need to make two intermediate calculations, each of which is interesting in its own right. First, update the expression for the “points” monthly payment to
![]()
After ![]() months, the amount of money you have given to the bank in the “no points” and “points” cases are
months, the amount of money you have given to the bank in the “no points” and “points” cases are
![]()
and
![]()
respectively. Because ![]() for reasonable8 values of
for reasonable8 values of ![]() (which is the whole reason you pay for points) this means that at no time over the duration of the loan will you have given the bank more money if you pay for points.
(which is the whole reason you pay for points) this means that at no time over the duration of the loan will you have given the bank more money if you pay for points.
This is a little counter-intuitive, partially because the phrase “buying points” make it seem like they’re independent of the loan amount. They’re not! You don’t have “down payment money” and “points money” and never the twain shall meet. It’s all just money9. That said, if the prospect of paying a little less every month gets you to increase ![]() in a way that reducing the loan amount does not, that’s fine, and the “wrong” method developed above is perfectly fine under those assumptions.
in a way that reducing the loan amount does not, that’s fine, and the “wrong” method developed above is perfectly fine under those assumptions.
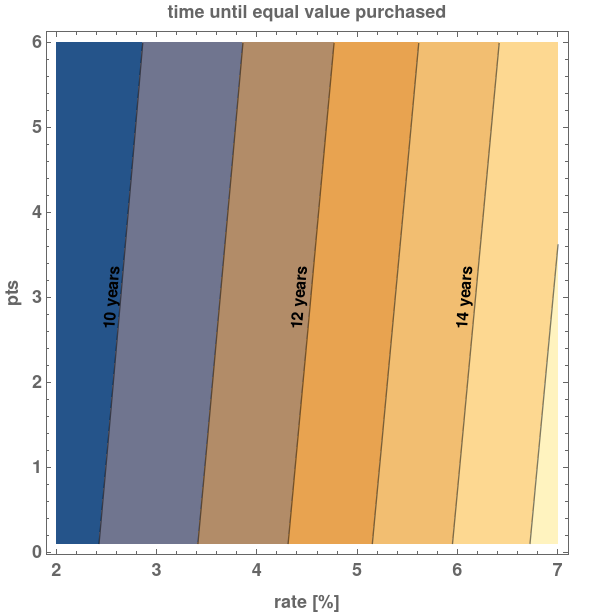
The points are not actually free though. After ![]() months, you will own a different amount of the house, depending on whether you have paid for points or not. Unlike the amount you’ve paid, there is a crossover in the “points” and “no points” cases, where after some number of months, you own more of the house having paid for the points. See Fig.2 below, followed by the equations.
months, you will own a different amount of the house, depending on whether you have paid for points or not. Unlike the amount you’ve paid, there is a crossover in the “points” and “no points” cases, where after some number of months, you own more of the house having paid for the points. See Fig.2 below, followed by the equations.
We get the above as follows. The amount remaining on the base rate loan in month ![]() is
is
![]()
and likewise, the amount remaining on the modified rate loan in month ![]() is
is
![]()
The amount of house you’ve bought after ![]() months is given by
months is given by
![]()
![]()
When you solve the equation
![]()
for ![]() , you get the crossover time shown in Fig.2. This is a lot longer than the payoff times suggested by Fig.1. It’s also not the whole story, since by the time you own the same amount of house in the “no points” case, you will have paid substantially less for that much house. Now that we have the building blocks, we can determine the payback time for points…
, you get the crossover time shown in Fig.2. This is a lot longer than the payoff times suggested by Fig.1. It’s also not the whole story, since by the time you own the same amount of house in the “no points” case, you will have paid substantially less for that much house. Now that we have the building blocks, we can determine the payback time for points…
The correct way
The net from the house purchase for the “no points” and “points” rates are
![]()
![]()
and so you find the payoff time by finding the month ![]() where
where
![]()
which is shown in Fig.3.
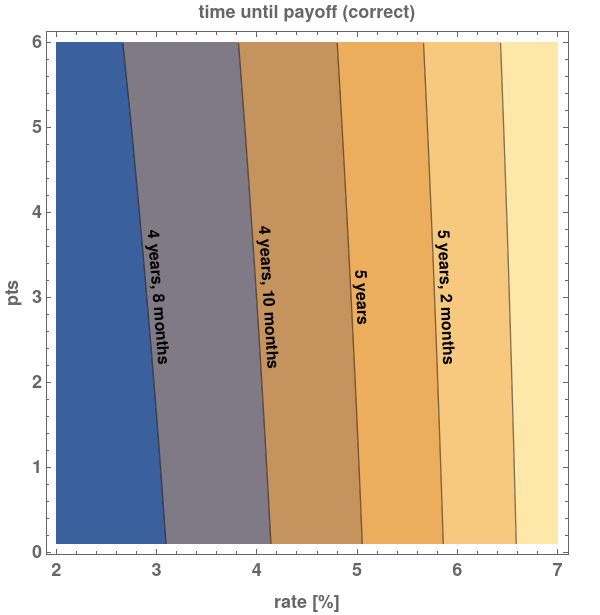
This is actually a slight improvement on the wrong method shown in Fig.1, meaning that the (easier) wrong method is conservative, a wonderful property for wrong methods to have. Unlike the wrong method, the payback time increases with increasing base rate. This makes sense, because the initial loan balance is larger. However, the correct method shows — like the wrong method — that the payback time increases as the number of points purchased increases. The most effective point or fractional point is therefore the first one, which makes it easier to discuss the effect of…
What you get for your points
At the beginning, we fixed the change in monthly rate that you get for a point as
![]()
which we can generalize to
![]()
where ![]() is the change in APR that you get per point. Because the most effective point available is the first one, we can fix
is the change in APR that you get per point. Because the most effective point available is the first one, we can fix ![]() to be a small fractional value to find the payoff time of the most valuable point at various base rates
to be a small fractional value to find the payoff time of the most valuable point at various base rates ![]() and changes in rate per point
and changes in rate per point ![]() . This is shown in Fig.4.
. This is shown in Fig.4.
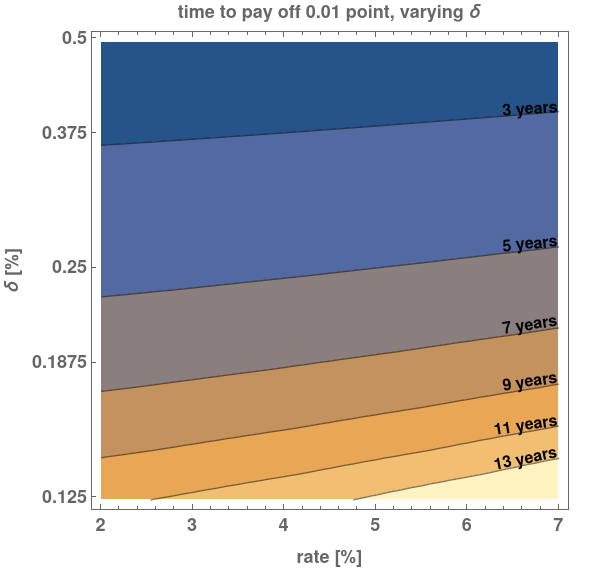
Unlike the changes in rate and number of points, changing the interest rate break you get per point makes a big difference. Changing the interest rate break from our nominal value of ![]() to
to ![]() more than doubles the time required to make the points profitable. A much smaller change, from
more than doubles the time required to make the points profitable. A much smaller change, from ![]() to
to ![]() makes between 17 and 24 months of difference in the payoff time.
makes between 17 and 24 months of difference in the payoff time.
Concluding remarks
There are some things that I had to leave out of the analysis of whether you should pay for points. Some of these things are not knowable, like what return rate you would get by putting the money you’re not using to pay for points into the stock market. (Zeroth order hypothesis: 10% nominal10, as long as you don’t do anything weird11 with it.) These calculations are valid for any term of fixed-rate mortgage, but because you can’t know what an adjustable rate mortgage (ARM) will do, these can only help bound the payback time of points on ARMs.
Other things are knowable for a given loan or lender, but there’s so little consensus that it’s hard to state generally how to engage with them. For example, many lenders require private mortgage insurance12 to be paid if the down payment is too small. Should you avoid buying points until your down payment is enough to avoid paying those premia? Probably, but there might be edge cases where it’s appropriate.
So, should you buy the points? Speaking against it is the tendency to overestimate how much you’ll approve of your current choices in the future,13 14 and the tendency of mortgage rates to move around over time, which increases the likelihood of refinancing.15 16 That said, if rates stay in their current range, and you’re pretty sure you going to be in that house for more than 5 years, and you don’t think you’ll refinance the loan in that time, then it’s a decent bet.
(Edit, 23-Oct-2022: Finished the followup article about refinancing. tl;dr: over the last 40 years, this was a good bet for the bank)
Questions or comments are best directed to @GlyphStory.
Featured image: Nick Young screencap by @jose3030, house from Wikimedia, cursed image manipulation by Aren with Mathematica.
- https://www.theatlantic.com/family/archive/2022/01/when-good-time-buy-house/621409/
- https://fortune.com/2022/01/28/home-price-growth-decelerates-again-forecast-models-say-peak-rate-behind-us/
- https://www.census.gov/construction/nrs/pdf/newressales.pdf
- aka, my digital and analog circle of acquaintances
- https://www.investopedia.com/mortgage-calculator-5084794
- I use “solve” throughout as shorthand for numerical root-finding.
- FRED, Accessed 17-Jan-2022
- If you set
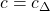 and solve for the rate change per point, you get ~0.007% over the whole (rate, point) space. This is at least an order of magnitude smaller than anything I’ve ever seen offered.
and solve for the rate change per point, you get ~0.007% over the whole (rate, point) space. This is at least an order of magnitude smaller than anything I’ve ever seen offered. - Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel, pleeeeze
- https://www.nerdwallet.com/article/investing/average-stock-market-return
- http://www.glyphstory.com/2019/08/20/the-generalized-death-cross-44701-exciting-ways-to-lose-money/
- https://www.consumerfinance.gov/ask-cfpb/what-is-private-mortgage-insurance-en-122/
- https://www.advdermatology.com/blog/statistics-surrounding-tattoo-regret/
- https://www.thestreet.com/mainstreet/news/americans-regret-new-mortgages
- https://fred.stlouisfed.org/series/MORTGAGE30US
- Does that last footnote read like a cliffhanger? Well spotted! I’m working on it, and I’ll link to it here when it’s done.