Can you leap tall mountains in a single bound?

Aren Hellum and Jesse Belden

“Fastest known time” (FKT) attempts are races, but less Chariots of Fire, more Cannonball Run. Each one is a distinct challenge; traverse of the Presidential Range, ascent of Whiteface, Lake Lansing loop, etc. They’re typically not mass or group start events, so an athlete can set out when ever they think the conditions suit them. Some routes are well-known and highly competitive, others might be a lower bar because of novelty¹. With races paused in 2020 because of the coronavirus, FKT attempts exploded as Type A endorphin-addicted weirdos² strap on their Stravas³ and try to outdo each other while maintaining social distancing.

“Everesting” is a class of FKT attempts where the athlete attempts to climb the height of Mount Everest (8848 m / 29029 ft). One option for this is to actually climb Mount Everest. Most folks find it more convenient to find a hill and ascend repeatedly until the total climb is equal to the height of Everest. There are time records for runners and cyclists, as well as ways to complete the challenge on a trainer within the spirit of the rules. Unlike most FKT challenges which measure the fastest time over a common route, Everesting allows the athlete to choose a route subject to the constraint on total elevation change.

The choice of route has some tradeoffs. If the gradient is too high, the athlete will be power-limited, but if the gradient is too low, the athlete is spending too much energy covering distance per meter ascended. It is interesting that the fastest cycling times are set around 14% gradient, while the best running times are all above 16%, and more commonly 25%+. This may be because of the different energetics of those sports, or it might just reflect that you tend not to pave long stretches of road with a 25% gradient because you will turn into a missile.

There is some room for interpretation about what might be considered an ascent, particularly on the cycling attempts:

If your descent includes a bit of climbing this still counts toward your total. Keep in mind that this is a climbing challenge, and routes with ‘kinetic gain’ should be checked via the everesting calculator first. The calculator has a built-in ‘check’ on descent elevation gain. You’ll know yourself from riding it in real life whether your chosen segment has a gain on the descent. We want to avoid ‘free metres’ where possible. A ‘rule of thumb’ should be applied when looking at a route with elevation gain on a descent or kinetic gain. If it feels like you are gaming the system, then you probably are!

Official Everesting rules, accessed 08-Aug-2021

This is reasonable–since the purpose of the challenge is for it to be challenging, you shouldn’t count climbing meters that you gained from coasting up part of your descent. Your authors are not reasonable, and consider the use of spacecraft and earth moving equipment to be fair game in the pursuit of sporting glory. Before we make this completely absurd, it is worth considering⁴ what is an ascent, really?

Consider an actual ascent of Everest, but one in which the climber begins walking from sea level in order to faithfully mimic the Everesting challenge. Just below the top, the climber does a belly-flop on the summit, never stands up, then descends. Assuming that the climber has a center of mass which is approximately one meter off the ground, the climber has moved their center of mass from one meter above sea level to exactly the height of Everest, plus a bit to account for torso thickness. If you define one Everest to be raising the climber’s center of mass by the height of Mount Everest, this belly-flop maneuver leaves you a bit short of the goal. This seems a little bit harsh.

What if we amend the definition, such that if the lowest point on your body has gone above some height, you have ascended by that amount? Consider next that you are Ryan Atkins, and you are interested in improving your already-preposterous Everesting time on the Chemin Thibault. You need to climb it 36 times, so you place a Slip-N’-Slide ⁵ with a banked turn at the top; this allows you to ascend the correct total height according to the new definition, but save a small amount of energy because your center of mass is never going above the summit. This probably won’t help your time unless you–again, Ryan Atkins–are mentally invigorated by the Summit-N’-Slide.

But here we see the outline of a potential loophole. What if there were more hills?

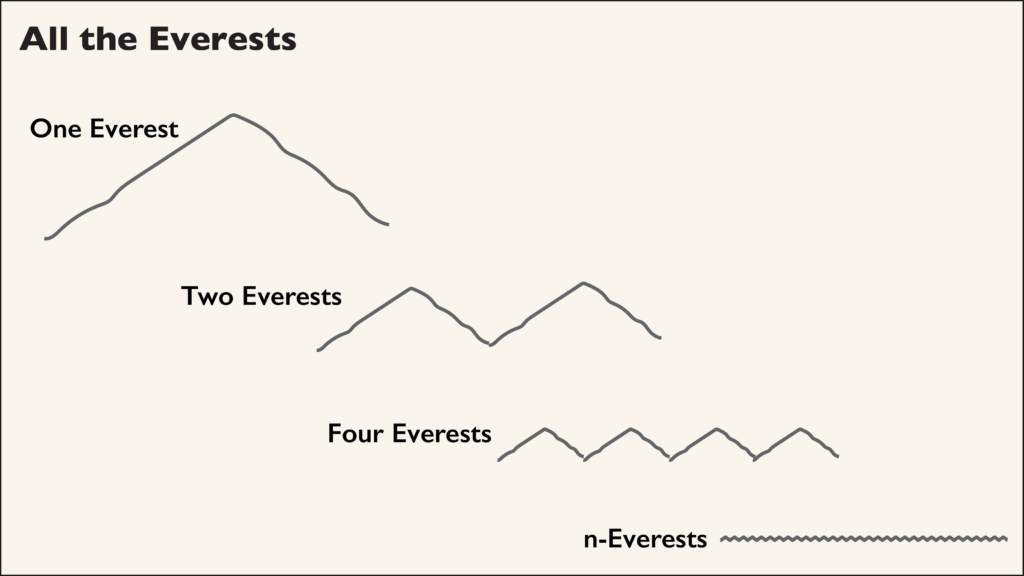
If you say that every obstacle you go over the top of counts for your ascent, you could “Everest” by introducing obstacles you can jump over, or better yet, run over. It is possible to show that what really matters is the aspect ratio of the tiny Everests you go over. The net ascent per distance traveled, , so if you you know the aspect ratios of your obstacles, you can calculate how far you would have to run to clear an Everest worth.

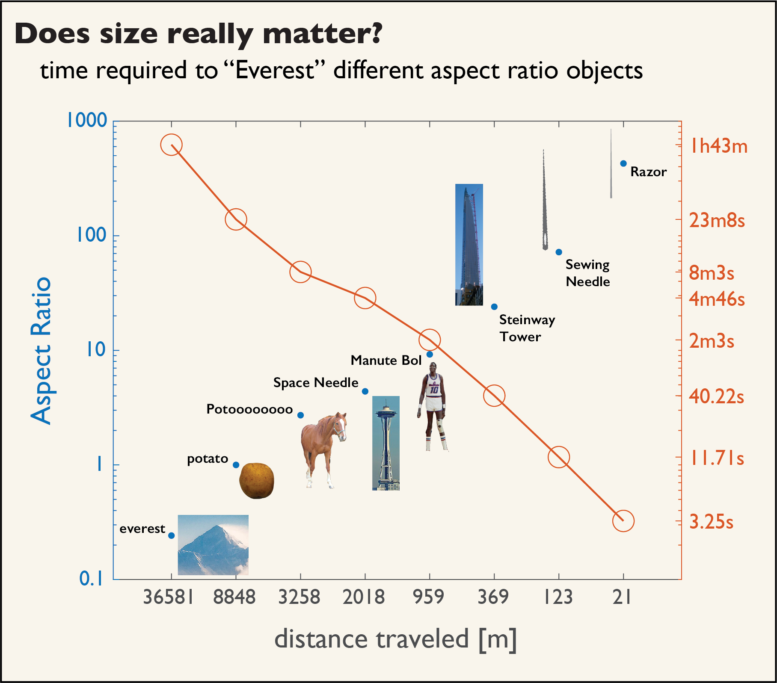
The distance you would need to travel in order to clear one Everest’s worth of tiny “obstacles” of various aspect ratios is shown on the left axis of the figure above. Notably: you can define what is allowed to be called a potato and Manute Bol is skinnier than the Space Needle. The time to travel that distance is on the right axis; while it would take 1h43m to run over a large number of tiny replica Everests, you could run over a densely packed forest of razors in 3.25s. I mean, you probably couldn’t, unless you are a world-class runner. On that note…

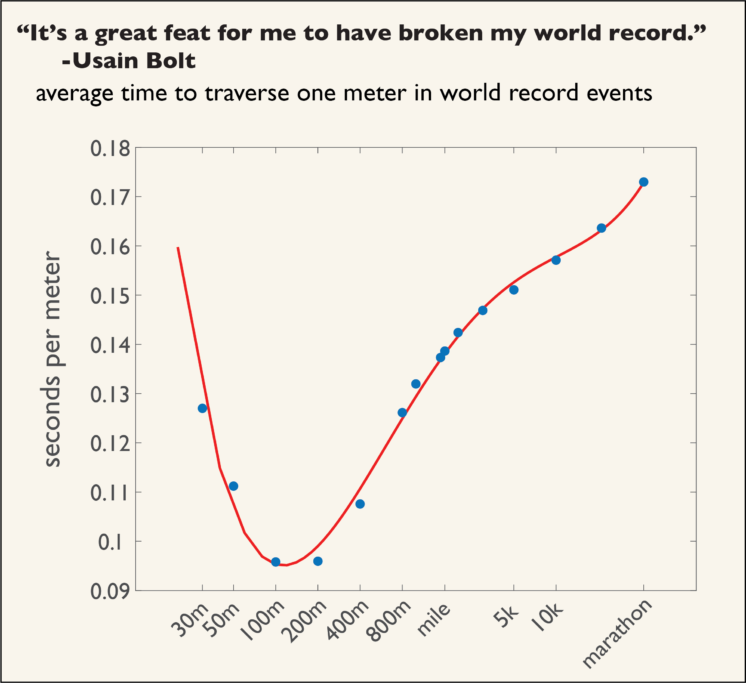
In order to go from horizontal distance traveled to time, you need to know how many seconds it takes to travel a meter. That time changes with the distance traveled, and is shown in the figure above. The curve fit used to make the conversion between horizontal meters and seconds is shown in red. It’s a fourth-order fit rather than an interpolation, because it needed to be well-behaved for the extrapolation from 30m to 21m. The latter is the distance to traverse an Everest’s worth of razor blades, and the former is the shortest rigidly-timed running record I can find. It was set by Churandy Martina in 2008, and he was racing dominos⁷.

One neat thing you can see on this plot is that distances less than 100m are slower on a per-meter basis than the 100m, because less of the race is run at top speed. Above 200m, the pace slows down because you’re getting tired. It looks like the times from 200m to ~1 mile are on a different curve than those above 1 mile. Probably this is a switch between energy systems and limits of pain tolerance/heat transfer/nutrition/???.

This is a bit out of scope here, but it does track with anecdotal experience implementing the Tabata protocol⁸. For those unfamiliar, the Tabata protocol is a high-intensity interval training protocol consisting of 8 rounds of 20 seconds of maximum work followed by 10 seconds of desperately gasping for air while you pray that your brain doesn’t overheat. That’s four minutes, which is about the same time as it takes to run a (very fast) mile. If you show me a person who does an honest Tabata and wants to go another round, I’ll show you a liar.

So, back to the central question: can you leap tall mountains in a single bound? If by that you mean, “Can you assemble a profoundly hazardous array of razor blades in such a way that the sum of their height is equal to the height of Mount Everest within a horizontal distance that a person could jump across?”, then the answer is, “No.” The 21 meters of horizontal travel required to “summit” Mount Tetanus is farther than a person has ever jumped⁹…unless you are willing to use a very long pole:

That’s right, kids! Fierljeppen¹² has entered the building! Fierljeppen, Frisian for “far-leaping”, is a Dutch sport whose origin lies in traversing the country’s canal-laced lowlands. To play, simply plant a very long pole into a canal bank, climb up it as fast as you can and fall on the other side. The still image above doesn’t really capture it. As Mr. Boersma explains in the linked video, the Dutch record is over 21.5 meters, just far enough to clear our carpet of razor blades. As the old saying goes, you ask a simple question, you get an answer that involves 145,000 razor blades and 12.5 meter carbon poles.

1. Jesse ran seven times up some hill in Providence, and I believe he had the record at some point?
2. It’s all love.
3. SPONSORED LINK? EH?
4. (massive bong hit)
5. SPONSORED LINK? EH?
6. https://en.wikipedia.org/wiki/List_of_world_records_in_athletics
7. Video evidence of Churandy Martina racing dominos.
8. Tabata et al. (1996). “Effects of moderate-intensity endurance and high-intensity intermittent training on anaerobic capacity and VO_2,Max“, Medicine and Science in Sports and Exercise 28(10).
9. The men’s long jump record is 8.95 meters, set by Mike Powell in 1991.
10. Denied.
11. Original due to Hans Dinkelberg.
12. Official site of the “Dutch summer sport”, translated to English.