Mo(to) drafting, mo(re) problems
by Aren Hellum and Jesse Belden
In stage 8 of the Tour de France, le grand espoir français Julian Alaphilippe was accused of drafting too closely behind a camera motorbike by fellow riders. While we tend to view post-race saltiness as a feature rather than a bug, it’s worth investigating just what physics says the rules ought to be about how close the cameras ought to be from the cyclists to avoid affecting the race. Because we’re experts and shit, that investigating will be done here.
The first thing to know is that drafting helps. A lot. In fact, a freeloading cyclist buried deep in the peloton uses only 10% of the power of a lone solo cyclist riding at the same speed.1 That means if a breakaway soloist is pumping out 400 Watts (W) of power, a domestique back in the bunch could be cruising at 40 W.2 But that’s in the mass of riders known as the peloton, what about a pair of riders?
For two wild cyclists out on the open road, the trailing rider gets a drafting benefit by riding in the aerodynamic wake of the leading rider. Most previous work on drafting3 4 5 had not really examined the effect of rider separation distances larger than a couple of meters. These works have, however, shown that if a rider’s front wheel is basically touching the rear wheel of the other cyclist, then the power output of the trailing rider is reduced by about 50%. But what if you don’t feel like wearing another cyclist’s ass cheeks for sunglasses that day?6 And more to the point of this discussion, what if you want to set a rule for how close one should be able to follow a motorbike?
According to Prof. Bert Blocken’s most recent data, the potential benefit of riding behind a motorcycle is non-negligible at distances on the order of tens of bicycle lengths. These effective drafting differences are much larger than I would have guessed from my own experiences failing to hang onto the wheel of unaccountably fast dudes who are definitely on the drugs.7 Per the link above, it was apparently a bit of a shock to Blocken as well, but when you examine his data in the context of a canonical turbulent wake, it makes some sense.
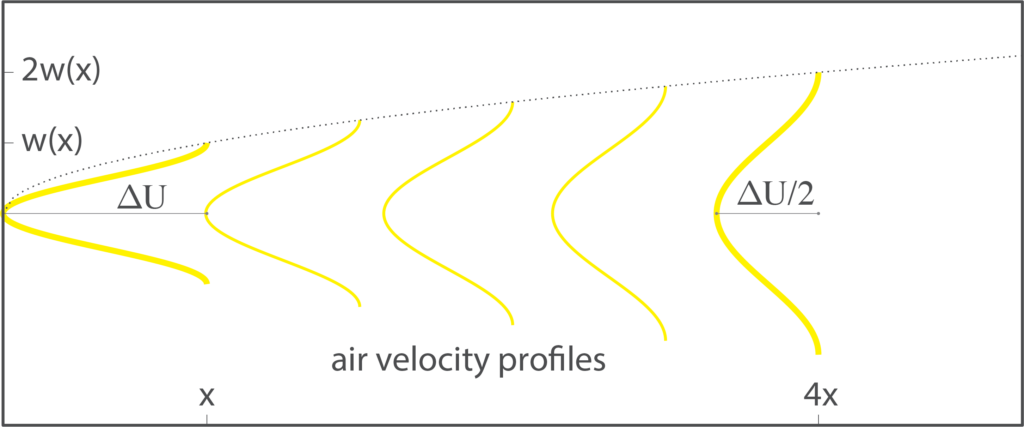
A self-similar velocity profile has the same shape at increasing distance, but scales according to the distance. In the case of a turbulent wake, the wake gets wider proportional to the square root of the trailing distance, i.e., ![]() . The wake also becomes “shallower” proportional to the reciprocal of the square root of the trailing distance,8 that is,
. The wake also becomes “shallower” proportional to the reciprocal of the square root of the trailing distance,8 that is, ![]() , where
, where ![]() is the shape of the wake and
is the shape of the wake and ![]() the free stream (or riding) speed. A cartoon of this type of wake is shown below. If you know the velocity profile as a function of position —
the free stream (or riding) speed. A cartoon of this type of wake is shown below. If you know the velocity profile as a function of position — ![]() — you can use that to estimate the drag reduction experienced by the drafting cyclist at any point in the wake. When you plot Blocken’s measured drag reduction behind a motorcycle against the distance, you see that it lines up reasonably well with a canonical wake, declining approximately as
— you can use that to estimate the drag reduction experienced by the drafting cyclist at any point in the wake. When you plot Blocken’s measured drag reduction behind a motorcycle against the distance, you see that it lines up reasonably well with a canonical wake, declining approximately as ![]() .
.
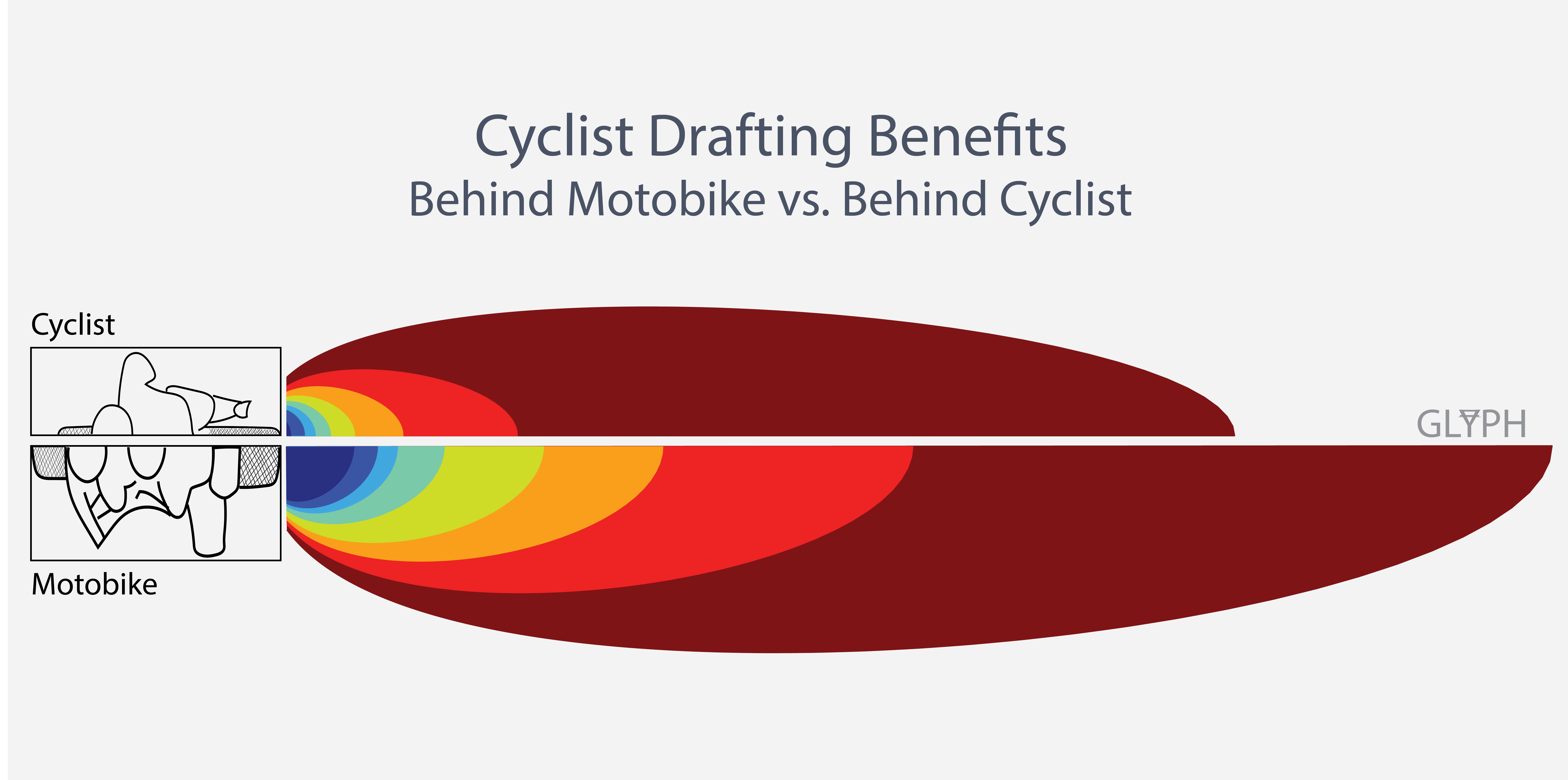
This self-similarity doesn’t hold immediately behind a cyclist or motorbike, but we have much more data in this near-wake region for cyclists, which allows us to assemble an estimate of drag reduction behind motorbikes and other cyclists, as shown in this figure:
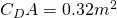 , which requires 510 Watts. In the wakes, the colors correspond to the required power as a function of position. These power numbers are compared with instances of average sustained power output of professional cyclists in varying conditions.
, which requires 510 Watts. In the wakes, the colors correspond to the required power as a function of position. These power numbers are compared with instances of average sustained power output of professional cyclists in varying conditions.So, how can we reconcile the long drafting region measured by Blocken with the personal experience of riding futilely through a wall of air when you fall out of someone’s draft? Some of it is likely mental, but while the drag reduction is measurable and strategically meaningful well behind the front rider, it does fall off rather quickly. Furthermore, if you were barely hanging on to begin with, going from 50% drag reduction to 5% is not going to help you.
- Blocken, Bert, et al. “Aerodynamic drag in cycling pelotons: new insights by CFD simulation and wind tunnel testing.” Journal of Wind Engineering and Industrial Aerodynamics 179 (2018): 319-337.
- No, this does not mean that you can ride in the Tour de France because you hit 100 W on your spin bike.
- Olds, Tim. “The mathematics of breaking away and chasing in cycling.” European journal of applied physiology and occupational physiology 77.6 (1998): 492-497. Anyone who uses the full word ‘mathematics’ in a journal paper title is a baller in our book.
- Barry, Nathan, et al. “The effect of spatial position on the aerodynamic interactions between cyclists.” Procedia Engineering 72 (2014): 774-779.
- Crouch, Timothy N., et al. “Riding against the wind: a review of competition cycling aerodynamics.” Sports Engineering 20.2 (2017): 81-110. See also sources cited within.
- Performance gains be damned. Sure, you will put that IV of dirty blood in your body, but you have some level of decency.
- Unsubstantiated, but whatthefuck man you look like Santa Claus whyyyy are you dropping me?
- Moser, Robert D., and Michael M. Rogers. “Direct simulation of a self-similar plane wake.” NASA TM108815 (1994).