…missed it by half a finger.

by aren · January 16, 2020

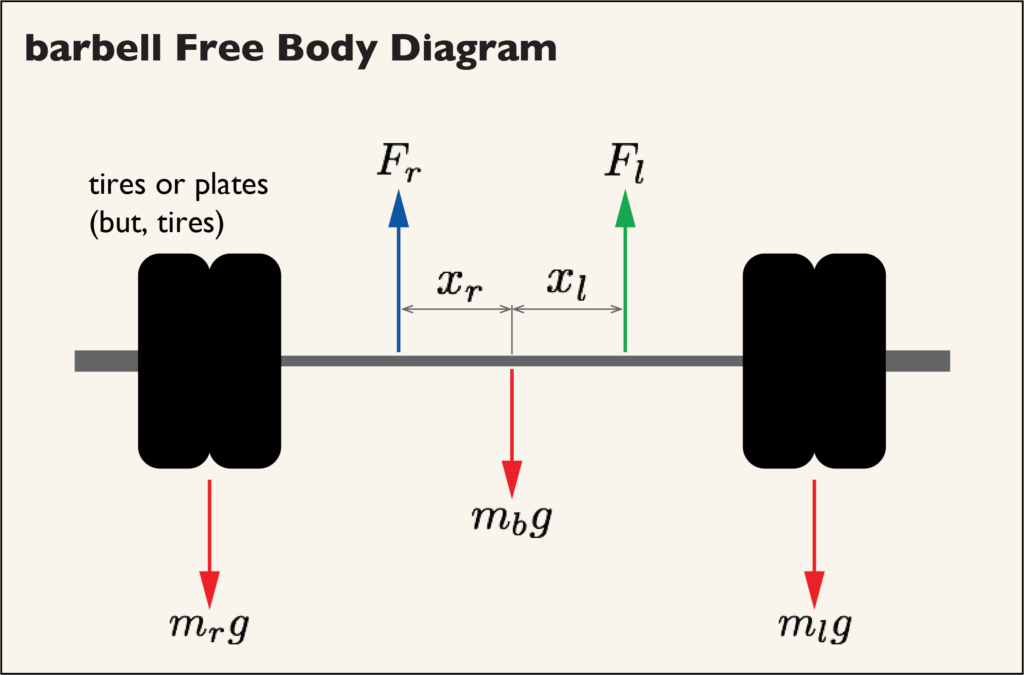
Have you ever looked at your hands? Like, really looked closely at them when you grab a barbell? Consider the barbell in the figure above, being held by strongman competitor and land monster Derek Poundstone. There is some weight on the left $(m_\ell g)$ , weight on the right $(m_r g)$ , and the weight of the bar $(m_b g)$ . Derek is pulling on the barbell with forces $F_\ell$ and $F_r$ .

We can simplify this a little bit by assuming that the barbell is loaded evenly such that $M = m_\ell + m_r + m_b$ and placing all of the weight at the center of mass. We can also make a cute little line drawing of the barbell and get rid of Derek, replacing his arms with force vectors. ¹ This is what we call a free-body diagram of the barbell. You’ll notice that we’ve placed two distances in the free body diagram, $x_\ell$ and $x_r$ , which indicate the distances from the center of mass to each of the lifter’s hands. I’m sure that won’t be important later.

To lift the barbell, you need to create enough force to accelerate the mass against gravity. We write this as follows:

$F_\ell + F_r = M (g+a_y). \quad (\rm{Force})$

The upward acceleration of the barbell $a_y$ on the right side simply means that the faster you want the barbell to move, the more force you have to apply. Also, if you place more mass on the bar, it will be more difficult to lift.² Also, if you do this on the moon, it is going to be easier. You’ve probably heard all of this before, even if you haven’t seen the math.

So, what about our weird insistence on writing out different forces for the left and right arms? There is another equation governing the motion of the barbell, which is that you need to keep it from rotating about its center of mass. We write this as

$F_r x_r - F_\ell x_\ell = 0. \quad (\rm{Torque})$

In plain English, this means that the torque placed on the center of mass by the right hand $(F_r x_r)$ must balance that provided by the left hand $(F_\ell x_\ell)$ or the bar will rotate. What happens if the bar rotates? Nothing good.

The force equation and the torque equation can be combined to solve for the left and right hand forces,

$F_r = \frac{M (g+a_y)}{1+\tfrac{x_r}{x_\ell}}$

$F_\ell = \frac{M (g+a_y)}{1+\tfrac{x_\ell}{x_r}}.$

The upshot of this is that your left and right hand are only providing the same amount of force if each one is exactly the same distance from the bar’s center of mass, such that $x_\ell = x_r$ . On a deadlift, this means that if your hands are different distances from the center, the grip on the hand closer to the center of mass will need to be stronger. It also means that you’ll have to provide a balancing torque through your core, which is an injury risk ³, and the load on your legs will be uneven in approximately equal proportion. This means that you will move less weight.

We can sort of quantify this by comparing the case when the right hand is set up a little off, closer to the center of the barbell ( $x_r<x_\ell$ ) to the ideal case where the setup is perfect ( $x_r=x_\ell$ ). A little quick algebra yields

$\frac{F_{r,off}}{F_{r,ideal}}\!=\!\frac{2}{1+\frac{x_r}{x_\ell}}\!\approx\!\frac{2}{1+\frac{19.65}{20.75}}\! \approx \!1.027$

That is, your right side will need to be about 3% stronger in order to lift this weight if you grip the barbell a little off-center than it would if it was gripped perfectly. Two questions are probably going through your head: (1) where the hell did those numbers for $x_r$ and $x_\ell$ come from, and (2) who gives a shit?

We’ll take those in order. The numbers came from one of our favorite papers⁴, the 2012 Anthropometric Survey of U.S. Army Personnel. Every so often, the Army takes lots of measurements on a large number of soldiers so that it can design uniforms, gear, vehicles, etc. In the last survey, they took 93 primary measurements and derived 41 more on a sample size of over 10000. It’s awesome.

Anyway, the biacromial width of a 50th-percentile male is 41.5 cm, which is a decent approximation of the total grip width on a deadlift. Let’s assume that the left hand is half that distance from the center, meaning $x_\ell=20.75 \rm{cm}$ . Estimating how far off your other hand might be is a little less straightforward, but I’d guess that most people can get within half the width of a finger without any great effort. The same 50th-percentile male, the one with 41.5 cm shoulders, has a hand breadth of 8.8 cm, so half of a finger width is approximately 1.1 cm. That makes $x_r=19.65 \rm{cm}$ .

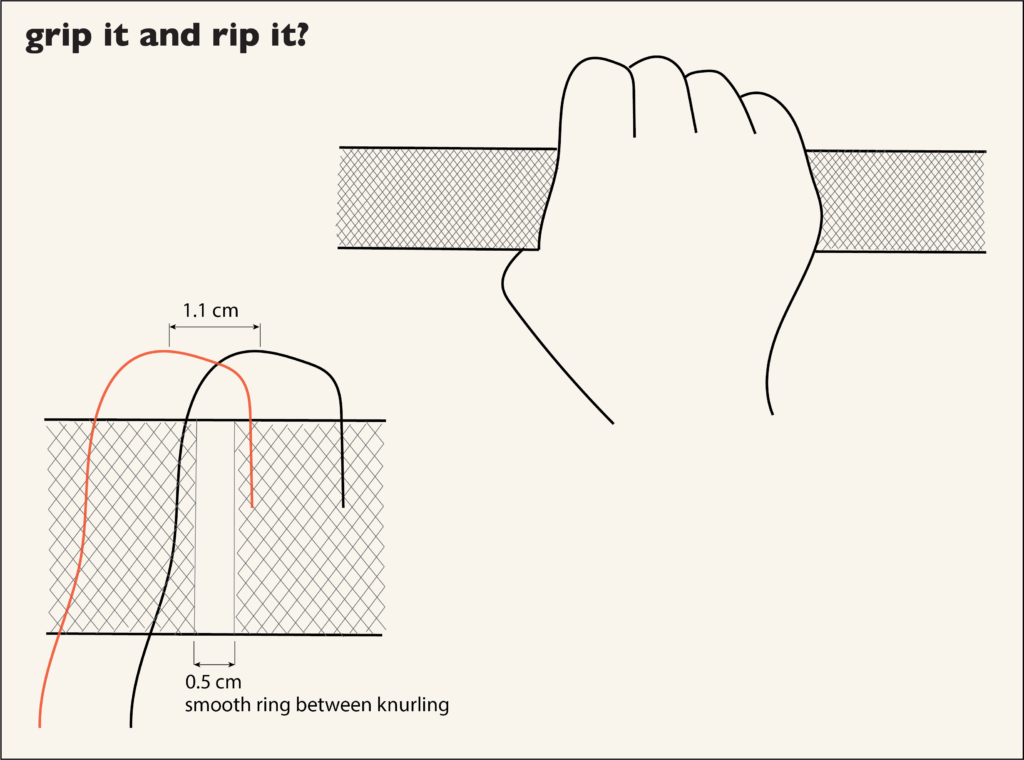
We can put this into some kind of context. An official Olympic barbell has two 0.5 cm gaps in the knurling, each 19.5 cm from the inside edge of the sleeve.⁵ We’ve superimposed a scaled 2.2 cm finger over this gap in the knurling. If you’ve ever used these rings as guides to make sure you’re grabbing the right place on the bar, as opposed to mimicking the pre-injury part of a WorldStar video⁶ ⁷, this should feel about right. You can get the smooth bit under the fat part of the finger, but probably not a lot more exact than that. If you’re judging the spacing visually in the middle of a knurled section, your accuracy might not be this good.

Okay, so who cares? The thing to take away from this should absolutely not be that you will be able to lift 2.7% more weight if you mark exact points on your barbell and lifting platform to ensure that your grip and feet are correctly placed to the micron. There are lots of things you could be fucking up that make more than 3% worth of difference.⁸ What these results might help you do is place bad days and good days in some context. If you can lose about 8 lbs on a nominally 300 lb. lift over something as simple as not looking at your hands twice, don’t conclude that your training has stalled after missing one lift. Similarly, while you’re looking at your hands twice, maybe look twice at a program that has you progressing in really small jumps–is your setup so tight that a 1.5% jump is outside the noise?

To close, a brief discussion of a good program, Jim Wendler’s 5/3/1.⁹ It prescribes intra- and inter-day jumps of 10% and 5% of base load, respectively. What’s interesting is the base load, which is 90% of the one-rep max (1RM). Why 90%, rather than 100% of 1RM? Better to let him explain:

Every time, without fail, when I asked someone what their one-rep max was, I’d get this: “Well, about three years ago I hit 365 for a triple, but that was when I was training heavier…” Most guys just don’t have a fucking clue. By using the 90%, I account for this bullshit.
Jim Wendler

Let’s say that your absolute best, ate-your-Wheaties, did-it-once-while-White-Rabbit-peaks lift is 350 lb. Your base lift in 5/3/1 would be 90% of that, 315 lb. How many half-fingers of error separates these two lifts?

$\!\!315 \rm{lb}\!\times\!1.027\!\times\!1.027\!\times\!1.027\!\times\!1.027$

$= 350.4 \,\rm{lb},$

so $\approx$ 4 half-fingers worth, distributed over every possible mistake you could be making. Maybe you have a devil-may-care approach to your grip spacing, or you favor your right leg out of the hole if you’re not looking at a mirror, or you initiate the second pull in your clean a hair early without good cuing, or you frequently lose some intra-abdominal pressure because of tiny farts. The difference between your best day ever and your everyday max is about 4 half fingers or tiny farts. Spend them as you will.

Aren Hellum and Jesse Belden

The forces are simplified to be only in the vertical direction, but would also have a lateral component along the vector of Derek’s arms. It doesn’t change the analysis below–don’t @ me.
Citation needed.
Fathallah, et al. (1998)
Gordon, et al. (2014)
IWF guidelines for sport equipment licensing
I’m not linking those, and you should love yourself enough to not search them out.
…fine.
Especially if you are Aren, whose deadlift setup is so loose as to be obvious to casual passers-by.
https://www.t-nation.com/workouts/531-how-to-build-pure-strength

…missed it by half a finger.

You may also like...

Recent Posts

…missed it by half a finger.

You may also like...

Le Tour de France Speed Spiral

Bobby Bonilla: fixed income investor

A brief update

Recent Posts