When are you animals going to let me buy some toilet paper?

It’s getting dire over here. Using Fermi estimation, let’s try to make a guess about how long it’s going to take for me to not-jokingly refer to the shower as “the standup bidet”. I live in the Greater South Kingstown/Narragansett megalopolis, home to approximately 46,000 Rhode Islanders, some fraction of whom are apparently eating toilet paper with Autocrat to salve their distress at the loss of Mr. Gisele Bündchen.
Fermi estimation is a method of using inputs you can easily approximate and dimensional analysis to arrive at reasonable answers. It can provide a first approximation or serve as a sanity check on a different detailed calculation. Sometimes you see it described as performing calculations only using the orders of magnitude, and sure, if you’re working with the Drake equation, you might just care about getting a reasonable number of digits in the solution. I typically employ it by canceling out multipliers that I don’t feel like keeping track of, which is why my notes frequently contain baffling assertions like ![]() = g.
= g.
So how many rolls of toilet paper are normally on the shelves in town? To get here, we first count the number of stores. Google Maps counts 4 drug stores, 3 grocery stores and 2 discount stores for a total of 9 stores, which we’ll round up to N=10 to account for convenience stores, gas stations, and the like. The aisle shelf space per store ![]() feet. This probably varies widely between stores, but it’s probably on the low end for grocery stores and a bit high for drug stores. Close enough for Fermi.
feet. This probably varies widely between stores, but it’s probably on the low end for grocery stores and a bit high for drug stores. Close enough for Fermi.
A roll of toilet paper is about 4 inches wide giving 3 rolls per foot. In halcyon pre-apocalypse times, I recall that the highest rolls of toilet paper were about as high as my head. The rolls are about 4 inches tall, so let’s call that 12 rolls high accounting for some gap off the ground and between shelves. Using a wild-ass-guess of 6 rolls deep, we get ![]() 200 rolls per aisle foot. This yields
200 rolls per aisle foot. This yields
![]()
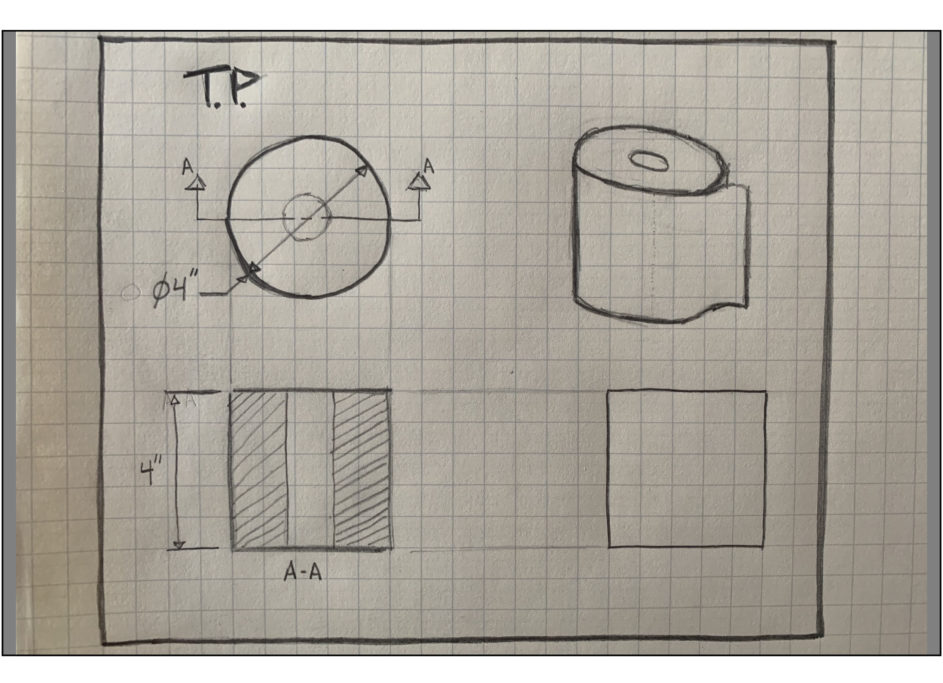
(hell yeah hand drawn iso view… still got it)
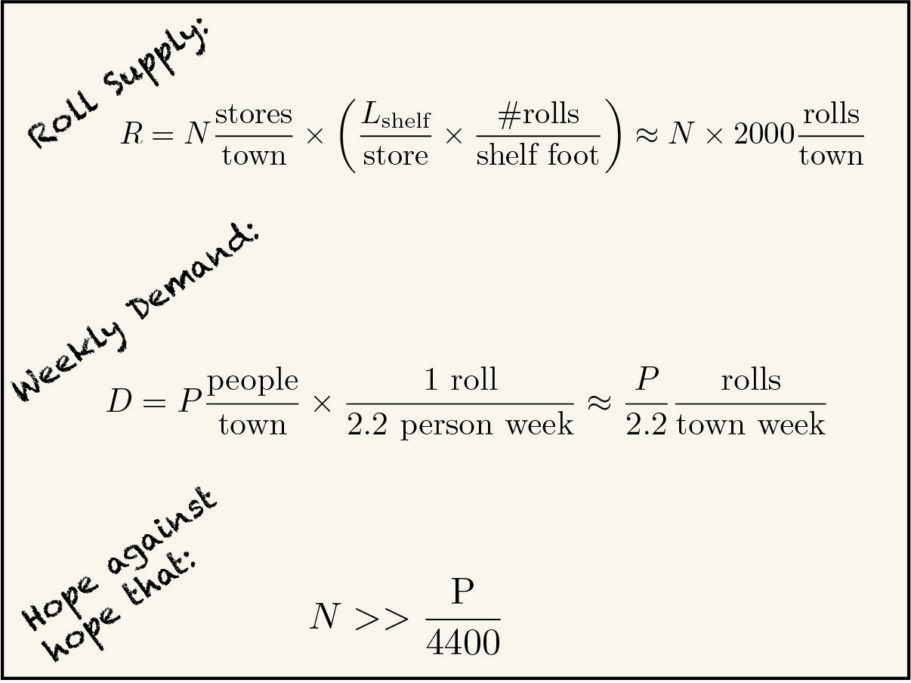
Next, we need some estimate of the number of rolls entering the system per week. Per wiki, Americans use approximately 23.6 rolls/capita yearly, or about 1 roll every 2.2 weeks, meaning that the average demand in town is
![]()
This is about the amount that has to enter town each week, meaning that there is normally about 1 week’s worth on the shelf. That is…much closer than I would have thought. We really are only one week from anarchy. (Or I really screwed up somewhere.) So this actually seems not too bad, right? Rolls in equal to rolls out, so no problem as long as noone is freaking out and buying a 10 years worth at a time. Strictly speaking, this is true no matter how many rolls were on the shelf to begin with, and can be generalized to your town:
Trouble is, toilet paper is typically sold in unit sizes greater than one roll, and people don’t normally buy it every week. I buy some this week, my neighbor buys some next week, Ted Leo buys some after that, and so on. It integrates out over a year, but the reserve can’t absorb a huge spike. Assuming 10 rolls per salable unit, we get U=2000 ![]() The average household size in Rhode Island is about 2.5, so let’s turn our 46000 Rhode Islanders into 18000 households. This leaves 16000 households currently deciding which of their towels they like the least. This calculus is a little more grim. At the current rate of flux into town, assuming everyone needs to buy TP, it could be 8 weeks before each household can do so, assuming noone hoards it.
The average household size in Rhode Island is about 2.5, so let’s turn our 46000 Rhode Islanders into 18000 households. This leaves 16000 households currently deciding which of their towels they like the least. This calculus is a little more grim. At the current rate of flux into town, assuming everyone needs to buy TP, it could be 8 weeks before each household can do so, assuming noone hoards it.
Stay safe out there, but seriously, stop buying all the bog roll. I’m down to two rolls, household of two. I’ve got 2.2 weeks, barring extraordinary measures.
Aren Hellum and Jesse Belden